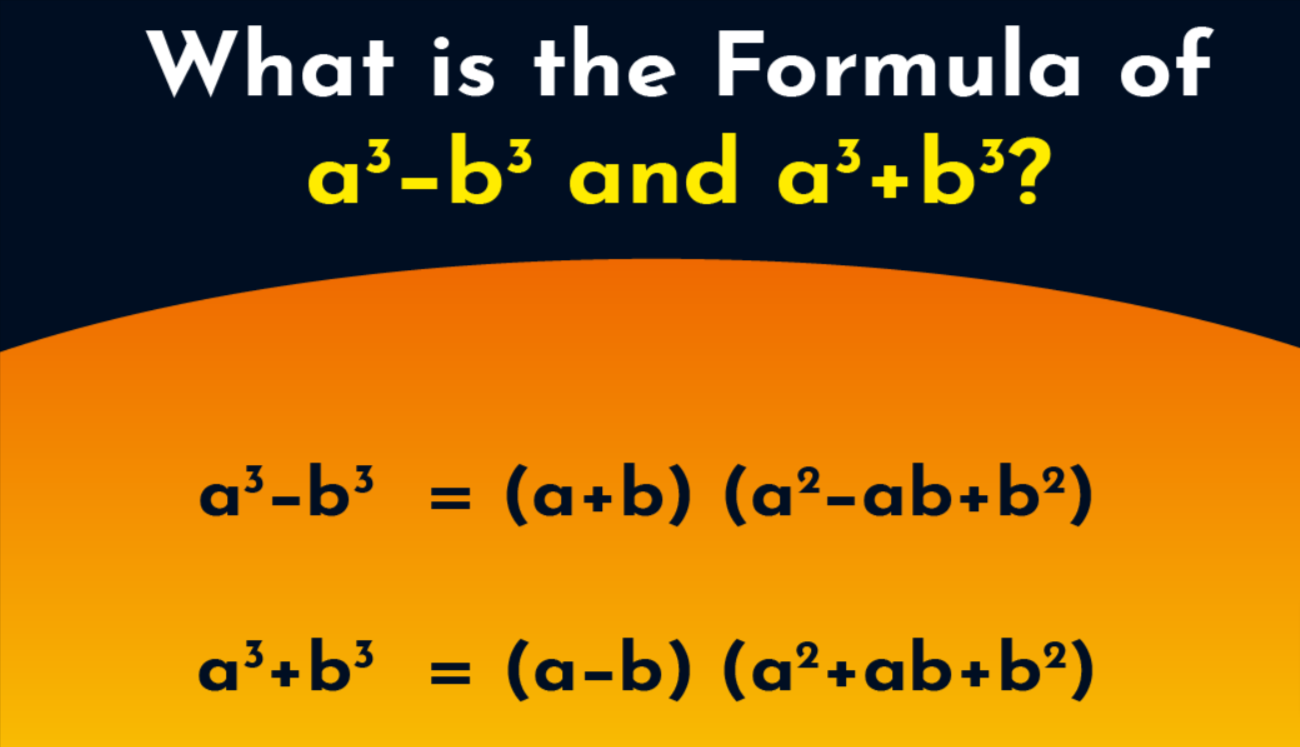The language of mathematics, which has been used for centuries in the world, has a in the form of equations, formulas and concepts. There are mathematical gems to be found is one of them is A3-B3 equation is: (a-b)(a2 + ab2 +) On the opposite other hand, the mathematical formula a3+b3 is which is 3ab(a + b) (a + b) (a + b)3 or a3 + b3 = (a2 ab + b2)(a + b). The term, also known by the name of the sum of cubes sparkles as an intriguing and intriguing algebraic expression. In this in-depth piece, we set off on an adventure to dive into the depths of this mathematical marvel. We will uncover its historic origins, the genesis of its algebraic identification the vast array of its programming and its long-lasting significance in the world of mathematics.
What is the formula a3-b3?
The A3-B3 formula is a simple yet incredibly charming mathematical expression, is an array of cubes each represented with the two terms A and. This mathematical jewel can be simplified into its simplest form:
a3-b3
The essence of the expression is in the illustration of 0.33 magnitude of two amazing real numbers: A and B. The act of combining A3 and B3 results in an final result that, despite the apparent simplicities, echoes throughout the mathematical universe.
The origins of the formula
The roots of the formula a3-b3 are deep in the history of mathematics and includes historical luminaries that include Diophantus and Fermat providing the inspiration for its research. But, it was transformed into the renowned Swiss mathematics professor Leonhard Euler who made tremendous contributions in the 18thcentury. Euler’s research did not just illuminated the mathematical system, but also began the process of constructing a complete understanding of its functions and their implications.
Understanding the Algebraic Expression
To unravel the secrets and techniques behind the formula a3-b3 it is necessary to look at the following:
- Both are real and real numbers, each having their own price.
- A3 represents the cube of the A.
- B3 represents the dice for B.
The process of combining B3 and A3 results in the cubes’ sum. This deceitfully accurate phrase is the entry point to a vast mathematical world in which the cube’s properties are interconnected and offer a greater understanding of their interactions inciting curiosity in mathematics.
Practical Applications
The potential of the formula a3-b3 is evident across a variety of mathematical worlds. It becomes a prized tool in algebraic manipulations, the concept of quantity, and even the thrilling field of cryptography. In the best instances, it acts as an essential element in solving complex mathematical problems. It also has an impact on the swarming of the mathematical world.
the formula a3-b3 in Geometry
Geometry, which is a world of sizes, shapes, as well as spatial dimension, doesn’t stay away from the enticement of the formula a3-b3. This formula reveals a nifty home for solving problems that are related to numbers. The dice of a number of frequently indicates the existence of a three-dimensional world geometric calculation, as well as the exploration of various forms benefit greatly from the software.
Variations and Expansions
The constantly evolving nature of mathematics is the reason for the exploration of expansions and variations of the A3-B3 formula. Mathematicians, with curiosity, have tapped into their imagination to create complexities and depths, uncovering new dimensions in the packages. Certain versions of the mathematicians have led to new discoveries.
Simplifying the Formula
Although using the A3-B3 formula may seem intimidating at first but mathematicians have not shrouded it in mystery. Different strategies were devised to make the formula simpler making it more to hand when solving mathematical issues. These streamlined techniques are vital to practical use and huge acceptance.
the formula a3-b3 In Real-Life Issues
The A3-b3 formula is frequently seen as a summary of mathematical concepts is a proof of its international importance. It is applicable to engineering, physics and even chemistry its software aids in the solution of real-world situations involving cubic dimensions. The bridge between the concrete and abstract emphasizes the practical significance of its software.
A Mathematical Insight
It is believed that the formula a3-b3 formula while simultaneously clearly displaying itself as an authentic addition, hides an intricate mathematical insight. It goes beyond the simple process of combining numbers, it invites mathematicians into a deeper understanding of the mathematical properties of cubes as well as their complex interactions. The enigma of cubes continues to fascinate mathematicians, and push them to unknown mathematical frontiers.
Importance in Modern Mathematics
In the current technological landscape In the current technological landscape, the A3-B3 equation is still regarded as a basic idea in math. The software has surpassed the traditional boundaries and are now affecting areas like the computer sciences and cryptography. The significance of this field in modern mathematics cannot be understated which is why it is so important in the modern age of technology.
Enjoy by using the the a3-b3 formula
In the realm of maths, pleasure and fascination usually go hands. Investigating your way through the a3-b3 formula opens a treasure trove of captivating puzzles and mind-teasing games. These challenging situations offer a enjoyable platform for college students and nerds to test their mathematical skills, while developing a love of the scenario.
Challenges and Complexities
As fascinating as the A3-b3 formula may be, it can no have to be a problem with its share of difficulties. Certain mathematical problems associated with this technique could be extremely complex and demanding modern mathematical strategies and methods to overcome. These problems, while in addition to being difficult, act as beacons that guide mathematicians to explore new areas of study.
Conclusion
The formula a3b3 formula and its incredibly simple and deep implications, stands as an example of the inexplicable appeal of math. From its humble origins to the current versions this mathematical beauty has been an object of curiosity and thinking in the mathematical world.