Its value for cos 180 degree is -1. The value of Cos 180 degree in Radians can be expressed as (180deg x 180deg x p), i.e., cos (p) or cos (3.141592. . . ). The article we’ll examine the ways to determine what cos is worth in 180 degrees using examples.
- Cos 180deg: -1
- Cos (-180 degrees): -1
- Cos 180deg in radians: cos (p) or cos (3.1415926 . . .)
What is the Value of Cos 180 Degrees?
The cos 180 degree is -1. Cos 180 degrees could be calculated using an equivalent to the angle (180 degrees) in Radians (3.14159 . . .)
We know that, using a degrees to radians conversion the radians in th = the number of degrees in x (pi/180deg)
is 180° = 180degrees x (p/180deg) the rad is 3.1415 or 3.1415 . . .
cos 180deg = cos(3.1415) = -1

Explanation:
When cos is 180° the angle 180deg lies along the negative x-axis. Thus cos 180deg value = -1
As the cosine function can be described as a regular function, we can define cos 180deg in terms of cos 180 deg = cos(180deg + 360deg + n) and n Z.
COS 180deg = 800deg = 540deg and so on.
NOTE: Since, cosine is an even function so cosine’s value is cos(-180deg) is cos(180deg).
Methods to Find Value of Cos 180 Degrees
The value of cos180deg is -1. The amount of cos180 deg by:
- Using Unit Circle
- Using Trigonometric Functions
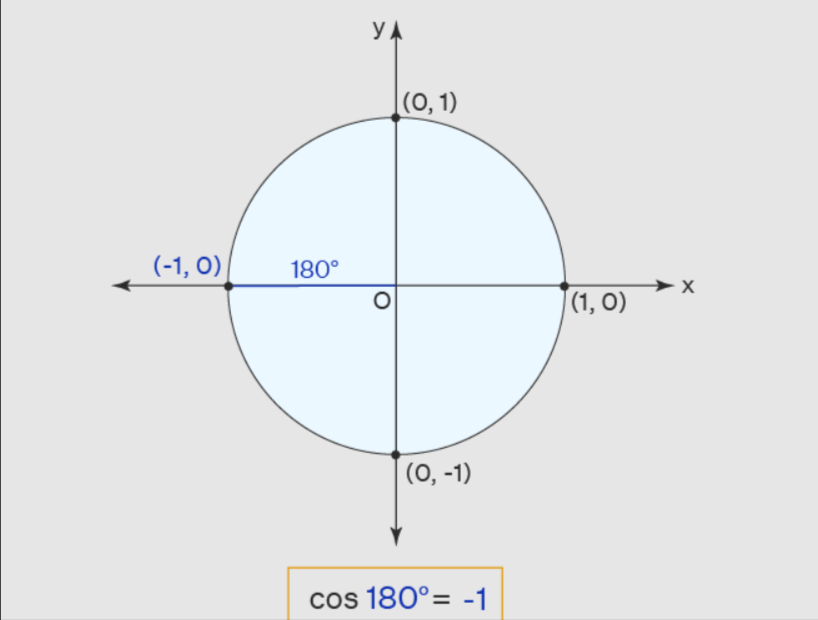
Cos 180 Degrees Using Unit Circle
To calculate how much cos180 degrees is, using this unit circle
- Turn ‘r’ clockwise to create a 180deg angle using the x-axis positive.
- The 180-degree cos is what is the x-coordinate(-1) that is the intersection point (-1 0, 0) of unit circle as well as the r.
Thus cos180deg = the value of x is -1.
Cos 180deg in Terms of Trigonometric Functions
By using trigonometry formulas we can define the cos 180 degree in the form of:
- +- (1-sin2(180deg))
- +- 1/(1 + tan2(180deg))
- +- +- 180deg/(1 + cot2(180deg))
- +-(cosec2(180deg) – 1)/cosec 180deg
- 1/sec 180deg
Note: Because 180deg is on the negative x axis, cos 180deg’s final number cos 180deg is negative.
We can make use of trigonometric names to describe cos 180deg in terms of,
- -cos(180deg – 180deg) = -cos 0deg
- -cos(180deg + 180deg) = -cos 360deg
- sin(90deg + 180deg) = sin 270deg
- sin(90deg – 180deg) = sin(-90deg)
Examples Using Cos 180 Degrees
- Example 1 Find how much 2 cos(180deg)/3 sin(-90deg).
Solution:
Utilizing trigonometric identities We can determine that cos(180deg) equals sin(90deg 180deg) = sin(-90deg).
= cos(180deg) = sin(-90deg)
The value of 2 cos(180deg)/3 sin(-90deg) = 2/3 - Example 2. Using the number of cos 180deg, find: (1-sin2(180deg)).
Solution:
We know that (1-sin2(180deg)) (cos2(180deg) = (cos2(180deg)) = 1.
= (1-sin2(180deg)) = 1 -
Example 3: Determine what is the sum of (cos2 90deg – sin290deg). [Hint: Use cos 180deg = -1]
Solution:
Utilizing the cos 2a formula,
(cos2 90deg – sin2 90deg) = cos(2 x 90deg) = cos 180deg
cos 180deg = -1
= (cos2 90deg – sin2 90deg) = -1